素粒子読本 樋口正人著 banner

小林悌二，齋藤曉 編

https://doi.org/10.50856/978-4-909624055

内容紹介

本書の特徴は，物質を構成する「素」の素を追求したい若い人達が，自然界の基礎にある階層性の探求がミクロ世界の基礎構造の解明へと展開していく現代素粒子物理学の流れの中へ，自然な構成を通して導かれるよう工夫されていることである。基礎となる電磁気学，相対性理論，量子理論の主要な骨格が前半で導入され，後半の主テーマである素粒子構造の追及への実験・理論の取り組みと，クォークを基とする美しい対称性がどのように探究され，構成されるかを有機的な展開で示される。必要な範囲の数学処方が丁寧に説明され，随所に著者長年の教育工夫が反映されている。読本という読みやすい形で素粒子物理学の世界を見通すことのできる本書は研究を志す人達のみならず，この世界の概観を知りたい多くの人達に大きなガイド役となるに違いない。

ダウンロード（オープンアクセス）・購入

初版 2020年10月10日 発行

製本版はこちらでお買い求め戴けます。（書籍版 ISBN 978-4-909624055）

発売はAmazon・楽天ブックス・三省堂書店のみとなっております。一般の書店ではお買い求めいただけません。

本書籍はCC BY 4.0で公開しており、PDF版はご自由にダウンロードいただけます。

PDF版ダウンロード

（2021年1月10日）「初版への追補・誤植の訂正」を掲載しました。

著者プロフィール

樋口 正人（ひぐち まさと）

1940年（昭和15年），宮城県に生まれる。1965年，東北大学大学院理学研究科原子核理学専攻修士課程修了。東北大学理学部助手を経て，1967年より東北学院大学工学部に勤務。1986年，東北大学から理学博士号の称号を授与される。1988年より東北学院大学工学部教授。その後，東北理工専門学校理事，高エネルギー加速器研究機構客員教授を兼任。長年，一貫して理論・実験の両面から素粒子物理学の研究に尽力，特に泡箱素粒子飛跡写真の解析プログラム構築等にも寄与，また教育を通して学生の素粒子・高エネルギー物理学への関心や研究意欲を高め，若手研究者や技術者の裾野を広げることに力を注いだ。2007年東北学院大学を定年退職。東北学院大学名誉教授。2019年6月没。

はじめに

素粒子物理学の歴史は，新しい思考と発見の歴史であった。「素」のものを求めて，ギリシア時代に端を発する原子の考え方や，トムソンによる電子の発見，湯川秀樹の中間子論の展開，リヒター・ティンなどによる新粒子ジェイ・プサイの発見など枚挙に暇がなく，歴史的には膨大な事項の蓄積がある。

本書では，数式は最小限とし，可能な限り言葉による説明を試みた。また，歴史上の事項の解説にページをさき，多少話題が古くなった部分もあるが，素粒子・高エネルギーに関心をもつものにとっては教訓的なものを含んでいるので，そのまま残した。

素粒子に関する話題は，大型加速器の稼動に伴い，事欠かない時代になってきた。2008年9月に稼動を開始したCERNの大型ハドロン衝突型加速器LHCでの成果が待たれる。この加速器では，現在広く受け入れられている標準理論の検証，宇宙の初期に粒子に質量を与えたといわれるヒッグス粒子の発見*とその波及効果，対称性から存在を予言されている超対称粒子の発見，強い力・電磁力・弱い力を統一的に説明できる超対称大統一理論の片鱗なりとも見えてこないかなどなど，その成果が大いに期待される。

* 補遺：その後2012年7月にヒッグス粒子はLHCで発見された。

本書成立の経緯について

本書は素粒子物理学を専門とする著者樋口正人氏が，大学における長年にわたる研究を背景とした講義，セミナー，講話をもとに，素粒子物理学の世界を，その基礎から現在の問題までの広範な話題について関連分野の発展と必然的関係に丁寧に触れながら非常に読みやすい形に構成して著したものである。

素粒子物理の発展の歴史，基礎となる数学，電磁気学，相対論，原子・原子核物理学などを基礎の準備内容として解説しながら，理論分野と実験分野の絡み合いについて丁寧に触れて，素粒子世界の理解に寄与してきた数多くの新概念の登場についてそのいきさつ，意味，果たして来た役割を詳しく記述している本書は，この分野の勉強，研究にこれから入ろうとする人にとって，素粒子世界理解の流れを概観し，その概要の把握が無理なくできるもってこいの内容と組み立てになっている。さらに，この分野に進んだ人にとってもその発展の流れを振り返って整理してみる上で大変有効な内容になっている。

著者は数年かけて本書の稿に取り組んでいたが，その間に病の兆しに出遇い，それを押して鋭意完成に努めた。一応の完成に達した稿について，著者の取り組み努力を見てきた東北大学理学部物理学教室同期で，その後も物理および関連の諸問題で絶えず意見を交わし合って来た荒川紘（元静岡大学），小林悌二（元東北大学），齋藤曉（元東京都立大学）の3人で稿を実らせる今後の方法について相談し合った。

先ず稿の点検を始めたが程なく著者の病状が進み，直接著者に確認したい具体的な記述箇所の数々について既に口頭や筆談でのやり取りができず，我々は大きな悩みを抱いた。しかし，著者の出版を前提とした熱心な原稿準備の経緯を踏まえると，上記の特徴をもった本稿を是非とも早く世に出したいとの思いが募る一方で，著者の快復を祈りながら点検と編集の作業を進め，成書としての出版に必要な種々の手続きの検討を重ねてきた。

この作業において，物理学書としての記述細部の統一性の点検，厖大な式および図版に関する修正・補修・再構成を小林，齋藤の主分担の下で慎重に進め，全体的整合性には荒川の通察を得て，かつ著者との直接応答ができない中での進捗状況をご家族に伝え，了解を得ながら完成を目指した。

原稿の整備を2019年5月にほぼ終え，これをもって2014年来入院闘病中の著者を見舞う予定でいたところ，6月初めに容体が急変し，帰らぬ人となってしまった。預かった稿の最終形を手に取ってもらえなくなった我々にとって返す返すも残念であった。

そこで成書化を急ぐこととし，具体的検討の中で幸い学術書刊行にユニークなアイディアを示しておられるやまなみ書房飯澤正登実氏に事情を説明し快諾を得ることができ，作業全般の労を引き受けていただき，度毎いただいた貴重なアドバイスのもとで念願の本書の刊行に漕ぎつけることができたのである。

本稿完成には，素粒子実験結果の幾つかのグラフ図版を著者が原典論文からコピー引用し，稿上に掲載予定箇所を指定していたものについて，その出典確認を素粒子実験でも著者と分野が近い東京都立大学物理学教室の汲田哲郎氏に依頼して，これを確定することができた。その作業を快く引き受けていただいた氏に感謝したい。また，本稿に当初なかった索引について作成の労をとっていただいた齋藤大吾氏に感謝したい。著者による直接の確認が得がたい状況下で推敲を行わざるを得なかった多くの補修・再構成箇所の責任は点検・編集を行った編者にある。

学友著者の冥福を祈りながら本書成立の経緯を記した。著者が元気だったころ，当時FORTRANカード時代だった東北大学大型計算機センターに大きなカードボックスを抱えて通い詰め，泡箱写真の解析プログラム作成に熱心に集中しており，時々その説明をしてくれた姿が今も思い出される。本書が多くの読者によって活用されるならば，念願していた著者の大きな喜びであり，かつ協力してきた我々もその喜びを分かち合えるものである。

2020年7月5日
編者 小林悌二，齋藤曉

目次

  • はじめに
  • 本書成立の経緯について
  • 第1章 物は何からできているか
    • §1.1 素粒子
    • §1.2 物の根源と大きさ
      • §1.2.1 疑いなく存在するのは人間
      • §1.2.2 ものの根源の変遷
    • §1.3 微小な世界
      • §1.3.1 階層構造
      • §1.3.2 細胞，分子，原子
      • §1.3.3 原子核と電子
      • §1.3.4 クォークとレプトン
    • §1.4 巨大な世界
    • §1.5 ものの最も根源となるものは
      • §1.5.1 真空
  • 第2章 素粒子たちは力をおよぼし合う
    • §2.1 相互作用は4つある
    • §2.2 力，場，媒介粒子
      • §2.2.1 電気力
        • 2.2.1.1 媒介粒子
        • 2.2.1.2 重力
        • 2.2.1.3 場と媒介粒子
    • §2.3 力はどこまで届くのだろうか
    • §2.4 電磁相互作用
    • §2.5 強い相互作用
    • §2.6 弱い相互作用
    • §2.7 重力
    • §2.8 反応の断面積
    • §2.9 極微の世界の単位は何だろう
      • §2.9.1 エネルギー
      • §2.9.2 質量
      • §2.9.3 運動量
      • §2.9.4 自然単位系
  • 第3章 素粒子を分類する
    • §3.1 分類の仕方
    • §3.2 スピンは整数か半整数か
    • §3.3 粒子の役割はどうであるか
      • §3.3.1 力を媒介する粒子
      • §3.3.2 物質を形成する粒子
        • 3.3.2.1 クォーク
        • 3.3.2.2 レプトン
      • §3.3.3 クォーク組成によるハドロンの分類
      • §3.3.4 質量の起源となった粒子
      • §3.3.5 ゲージ原理
      • §3.3.6 質量はヒッグス機構とともに
        • 3.3.6.1 カイラル対称性の破れ
        • 3.3.6.2 物質の質量
  • 第4章 相対論のはじめ
    • §4.1 ガリレイ変換とローレンツ変換
      • §4.1.1 ガリレイ変換
      • §4.1.2 真の変換は何であろうか
      • §4.1.3 アインシュタインの特殊相対性原理
      • §4.1.4 ローレンツ変換
      • §4.1.5 ローレンツ・フィッツジェラルドの短縮
      • §4.1.6 時間の遅れ
    • §4.2 4元ベクトル
      • §4.2.1 斜交座標系
      • §4.2.2 世界線
      • §4.2.3 4元ベクトルの成分
      • §4.2.4 4元ベクトル
    • §4.3 4元ベクトルのスカラー積
      • §4.3.1 スカラー積
      • §4.3.2 計量テンソル (metric tensor)
    • §4.4 運動量とエネルギー
  • 第5章 続相対論的・量子論的粒子
    • §5.1 運動方程式
      • §5.1.1 相対論的運動方程式
      • §5.1.2 種々の物理量の関係
      • §5.1.3 量子論的運動方程式
    • §5.2 相対論的波動方程式
  • 第6章 素粒子の世界を探るには
    • §6.1 素粒子の世界を探る
      • §6.1.1 高エネルギーの必要性
        • 6.1.1.1 物質の分解
        • 6.1.1.2 新粒子の生成
        • 6.1.1.3 分解能の向上
    • §6.2 素粒子の検出
      • §6.2.1 荷電粒子
        • 6.2.1.1 電離，励起
        • 6.2.1.2 チェレンコフ光
        • 6.2.1.3 シャワー
      • §6.2.2 中性粒子
    • §6.3 素粒子を見る——測定器の種類
      • §6.3.1 (A) 電気的な検出
      • §6.3.2 (B) 光による検出
      • §6.3.3 (C) 飛跡による検出
  • 第7章 粒子の加速
    • §7.1 加速原理
    • §7.2 加速器の種類
      • §7.2.1 コッククロフト・ウォルトン (Cockcroft-Walton) 型
      • §7.2.2 ヴァンデグラフ (Van de Graaff) 型
        • 7.2.2.1 タンデム・ヴァンデグラフ型
      • §7.2.3 サイクロトロン (Cyclotron)
        • 7.2.3.1 ビーム集束
        • 7.2.3.2 シンクロサイクロトロン (Synchro-cyclotron)
      • §7.2.4 ベータトロン (Betatron)
        • 7.2.4.1 ベータトロン振動
    • §7.3 シンクロトロン(Synchrotron)
      • §7.3.1 概要
      • §7.3.2 位相安定の原理
      • §7.3.3 高周波加速
      • §7.3.4 強集束の原理
    • §7.4 線形加速器
    • §7.5 衝突型加速器
      • §7.5.1 ルミノシティ
  • 第8章 マクスウェル方程式の美しさ
    • §8.1 いくつかのベクトル演算
    • §8.2 マクスウェル方程式
    • §8.3 ゲージの凍結
      • §8.3.1 クーロンゲージ (Coulomb gauge)
      • §8.3.2 ローレンツゲージ (Lorentz gauge)
    • §8.4 マクスウェル方程式の4元ポテンシャル表示
  • 第9章 ディラック方程式を解く
    • §9.1 スピノル
    • §9.2 スピン行列
    • §9.3 ディラック方程式
    • §9.4 ディラック方程式の解
      • §9.4.1 静止状態の粒子
      • §9.4.2 ディラック方程式の一般解
  • 第10章 𝐶,𝑃,𝑇変換の対称性
    • §10.1 物理法則の不変性
    • §10.2 𝐶𝑃𝑇定理
    • §10.3 パリティ変換(𝑃変換)
      • §10.3.1 パリティの固有値
      • §10.3.2 パリティ非保存の問題
    • §10.4 荷電共役(荷電反転，𝐶 変換)
    • §10.5 𝐶𝑃変換
    • §10.6 時間反転(𝑇変換)
    • §10.7 中性子，原子による 𝑇 変換の検証
  • 第11章 クォーク 仮想から実在へ
    • §11.1 坂田モデル
    • §11.2 クォークモデル
      • §11.2.1 クォークモデルの考え方
      • §11.2.2 群
        • 11.2.2.1 回転群
        • 11.2.2.2 ユニタリー群
      • §11.2.3 中間子族
        • 11.2.3.1 桜井の考察
      • §11.2.4 重粒子族
    • §11.3 カラー(color)のSU(3)
      • §11.3.1 カラー荷
      • §11.3.2 相互作用の強さ
      • §11.3.3 カラーと強い相互作用
      • §11.3.4 シールド効果
  • 第12章 新世代のクォークと実験的検証
    • §12.1 第2世代，第3世代のクォークの発見
      • §12.1.1 第2世代クォーク
        • 12.1.1.1 背景(あるとすれば)
        • 12.1.1.2 𝐽/Ψ の発見
        • 12.1.1.3 なぜチャームであるか
      • §12.1.2 OZI則（大久保 − ツバイク − 飯塚規則）
      • §12.1.3 チャーム・クォークの質量とチャーモニウム
    • §12.2 𝑏,𝑡クォーク
      • §12.2.1 𝑏クォーク
      • §12.2.2 𝑡クォーク
    • §12.3 時間的光子による粒子発生
    • §12.4 電子・陽電子衝突反応におけるハドロン発生
    • §12.5 クォークとレプトンに第4世代はあるか
    • §12.6 標準モデルによる計算
      • §12.6.1 𝑅
      • §12.6.2 𝑊,𝑍の質量
      • §12.6.3 世代(generation)数
        • 12.6.3.1 加速器実験
        • 12.6.3.2 その他の実験
  • 第13章 負エネルギー粒子
    • §13.1 発端
    • §13.2 ディラックの空孔理論
    • §13.3 電荷密度，電流密度
    • §13.4 負エネルギー状態
    • §13.5 反粒子を含むファインマン図
    • §13.6 反粒子のアイソスピン
      • §13.6.1 アイソスピン
      • §13.6.2 反粒子のアイソスピン
        • 13.6.2.1 クォークの合成系
    • §13.7 この宇宙の反粒子は何処へ行ったか
  • 第14章 回転運動とスピン
    • §14.1 軌道角運動量
    • §14.2 スピン
    • §14.3 角運動量の合成
      • §14.3.1 全角運動量
      • §14.3.2 二つの状態の合成
  • 第15章 ゲージ変換とは
    • §15.1 不変性，対称性
    • §15.2 ゲージ原理
    • §15.3 ラグランジアン
    • §15.4 電荷の保存
    • §15.5 局所ゲージ変換
    • §15.6 場と運動方程式
    • §15.7 U(1)対称性
  • 第16章 標準理論（電弱統一理論）
    • §16.1 標準理論の発展
      • §16.1.1 発端
      • §16.1.2 弱アイソスピン
      • §16.1.3 U(1)𝑌 ⊗ SU(2)𝐿 とゲージボソン
    • §16.2 標準理論の粒子
    • §16.3 電弱統一理論（標準理論）
    • §16.4 中性ゲージボソン
    • §16.5 対称性の破れ
      • §16.5.1 大域的対称性の破れ
        • 16.5.1.1 あからさまな対称性の破れ
        • 16.5.1.2 自発的対称性の破れ
      • §16.5.2 ヒッグス機構
      • §16.5.3 質量0の粒子が質量をもつ例
  • 第17章 標準理論に続くもの
    • §17.1 大統一理論
    • §17.2 陽子は崩壊するか
    • §17.3 大統一エネルギー
    • §17.4 階層性の問題
    • §17.5 超対称性理論
      • §17.5.1 暗黒物質
  • 索引
    • 用語索引
    • 人名索引
  • 談話
    • 談話1 物質の根源
    • 談話2 時空の関係
    • 談話3 ルミノシティの実用単位
    • 談話4 パリティの固有値

ライセンス

この書籍はクリエイティブ・コモンズ 表示 4.0 国際 ライセンスの下で提供しています。
クリエイティブ・コモンズ・ライセンス

初版への追補・誤植の訂正

［追補］

p.16 ハッブル法則の現行呼称について

1927年に初めて宇宙膨張を提唱し膨張速度の予想値を求め，目立たない雑誌の論文*で示していたGeorges H.J.É. Lemaîtreの功績を称えて，XXX IAU General Assembly（第30回国際天文学連合総会）（2018年8月20日～31日）でHubble Law（ハッブル法則）をHubble–Lemaître Law（ハッブル−ルメートル法則）に改称することが提案[決議案PDF]され，2018年10月26日に正式決定した。[投票結果PDF]

* Lemaître, G. (1927). “Un univers homogène de masse constante et de rayon croissant, rendant compte de la vitesse radiale des nébuleuses extra-galactiques.” Annales de la Société Scientifique de Bruxelles A47(47): 49–59.
英訳：Lemaître, G. (2013). “Republication of: A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulae.” General Relativity and Gravitation 45(8): 1635–1646.

［誤植の訂正］

  • p.12 脚注2 §3.3.2の脚注参照。 → §3.3.2 表3.3中の注記参照。
  • p.35 上から1行目 $\hbar / 2 \pi$ → $\hbar$
  • p.40 式(2.28)の上の行 $\hbar = 6.6 \times 10^{-25} \mathrm{MeV}\cdot\mathrm{s}$ → $\hbar = 6.6 \times 10^{-25} \mathrm{GeV}\cdot\mathrm{s}$
  • p.62 チャーム・メソンの行 $\bar{D}^0=\bar{c}d$ → $\bar{D}^0=\bar{c}u$
  • p.62 チャーム・バリオンの行 $Λ_{c}^{0}=udc$ → $Λ_{c}^{+}=udc$
  • p.150 下から9,8,7,6,5行目 デー → ディー
  • p.155 下から3行目 リヴィングストンM.S.(Livingston) → リヴィングストン(M.S.Livingston)
  • p.171 上から8行目 電荷$e$の荷電粒子が → 電荷$q$の荷電粒子が
  • p.225 下から7行目(1箇所), 8行目(2箇所) ストレジネス → ストレンジネス
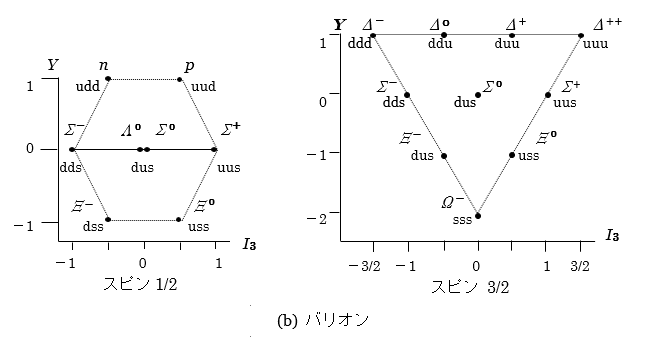
  • p.236 図11.2(b)バリオン （右図）スピン3/2 $I_{3}$の目盛欠落の修正 （左図）$\Lambda^{0}, \Sigma^{0}$のクォーク構成 $uus$ → $dus$，$\Sigma^{+}$のクォーク構成 $uds$ → $uus$
    図11.2(b)右図 rev2
  • p.270 上から5行目 ワインバーグー → ワインバーグ
  • p.271 脚注（2箇所） et. al. → et al.
  • p.280 下から2行目 $(dsc)$である$\Sigma_{c}$ → $(ddc)$である$\Sigma_{c}$
  • p.281 上から7行目 $\Sigma_c$の組成 $dsc$ → $ddc$
  • p.291 式(12.41) $B^{0}(b\bar{d}), \bar{B}^{0}(\bar{b}d)$ → $B^{0}(d\bar{b}), \bar{B}^{0}(\bar{d}b)$
  • p.294 下から2行目 2-jetイベントれとなるが → 2-jetイベントとなるが
  • p.294 図12.20 紙面左から右への時間進行を前提として，反粒子線の矢の向きを修正
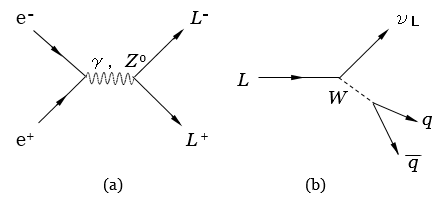
    図12.20 rev2
  • p.300 表12.1 最初の行 $\nu_{2}, \nu_{\mu}, \nu_{\tau}$ → $\nu_{e}, \nu_{\mu}, \nu_{\tau}$
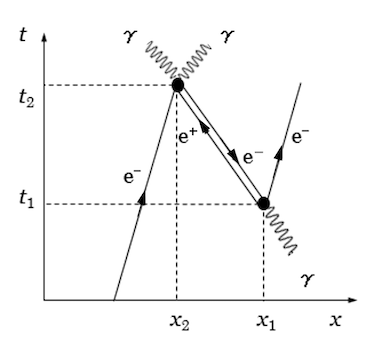
  • p.313 図13.7 入力側の光子の矢の向きが時間軸に対して逆方向であった。時間軸に沿って光子の進行方向は自明ゆえ、光子走行の矢自体を削除
    図13.7 rev2
  • p.315 上から5行目 加算的量子数が保存量であるならば（バリオン数，レプトン数，電荷など）は， → 加算的量子数が保存量であるならば（バリオン数，レプトン数，電荷など），
  • p.347 上から6行目 電荷の保存側 → 電荷の保存則
  • p.386 式(16.43) 追記：$\lambda$の表式は有理化CGS単位系（ガウス有理化）を用いている。
  • p.388 式(16.50) $$-\frac{\epsilon\mu}{c^2}\frac{\partial^2 \boldsymbol{B}}{\partial t^2}$$ → $$-\frac{\epsilon}{c^2}\frac{\partial^2 \boldsymbol{B}}{\partial t^2}$$
  • p.404 用語索引 KEK（高エネルギー加速器機構） → KEK（高エネルギー加速器研究機構）
  • p.406 用語索引 クォーク, 11, 13, 22, 36, 56, 234, 234, 373 → クォーク, 11, 13, 22, 36, 56, 234, 373
  • p.407 用語索引 質量数, 10 → 質量数, 9, 10
  • p.408 用語索引 多線比例計数管 → 多線比例計数箱
    • （編者追補）電極線を囲んだ計数管を多数線状に配列しchamber(箱)として構成されたMWPC形式のものなので普通は「計数箱」の呼称が使われている。計数管の一形式には違いなくその呼称も使われることがあるが，計数装置を専門とする著者がp.139で意識的に比例計数管と多線比例計数箱を区別して並べているので，文中の通り計数箱としておきたい。
  • p.409 用語索引 チェレンコフ検出器, 139 → チェレンコフ検出器, 140
  • p.411 用語索引 フレーバー(flavor), 57, 234, 256 → フレーバー(flavor), 57, 235, 256